Bridge Out
-
ChallengeBackgroundMethodsSimulationAssessment
Imagine that you are the mayor of a small city that is comprised of several islands connected by bridges. You want to organize a parade to celebrate a famous astronaut that was born in your town, Rich Lidbutter. Your challenge is to devise a route around the city that goes through every road, because you want all the citizens of the town to experience the parade. However, you don’t want them to get bored, so you can only travel through each bridge once. The parade is today, so grab your baton and march off!
Who is Leonhard Euler?
Leonhard Euler (pronounced "oiler") was a Swiss physicist and one of the greatest mathematicians of all time. Euler worked in many areas of mathematics, including geometry, algebra, and physics, just to name a few. Although he lived in the 18th century, his work and discoveries still apply to us today. For example, he introduced the concept of a function, and also made the popular the use of notations like e for the base of the natural logarithm (also known as Euler's Number).What is Euler's Theorem?
Euler's Theorem is a theorem that applies for all polyhedrons. Polyhedrons are 3D geometric shapes like a triangular pyramid, cube, pentagonal prism, etc. Euler's Forumla is that if you subtract the number of edges with the number faces plus the number of vertices the answer is always 2, or F+V-E=2. For example, in the first picture below, there are five faces, the base plus the four triangular sides. There are also five vertices, the apex, and the four corners of the base. The edges add up to eight, there are four that connect the four triangles together and an additional four that connect each triangle to the base. Euler's Formula is: 5+5-8=2 which is correct in this case.What is amazing is that his formula works for every polyhedron from simple ones to more complicated ones like a dodecahedron as pictured in this second image below.)
http://www.mathsisfun.com/platonic_solids.html
What is a practical application of Eulers' Theorem?
Euler's Theorem works on all polyhedron and due to this formula, scientists were able to predict a molecule's structure. Chemists found a new molecule with the exact weight of 60 carbon atoms. They knew that the number of vertices was 60, and that three were 90 bonds between them. Using Euler's formula, they predicted that the molecule had 32 faces which is a truncated icosahedron as pictured below. This is also the shape of a soccer ball which has both hexagons and pentagons in its geometric shape.)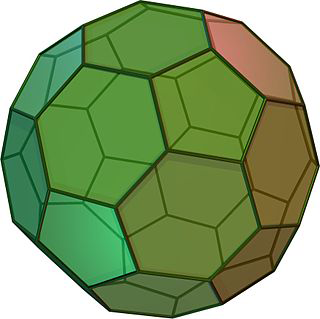
http://en.wikipedia.org/wiki/Truncated_icosahedron
What is discrete mathematics?
Discrete mathematics is the study of discrete mathematical structures. These structures have distinct separated values. There are no continuous structures like the long range of numbers between each integer. For example, from 1 to 2 there are decimals like 1.25, 1.5, 1.33333 etc. Discrete mathematics deals with only integers 1, 2, 3...and other discrete structures. Another example are logic statements where there is only a true or false and nothing in-between.What is graph theory?
Invented by Euler, graph theory is the study of graphs, which are mathematical structures of nodes that are connected by vertices. The connection demonstrates a relationship between the nodes and how they are connected. Graph theory is used in many applications such as computer science, chemistry, biology, and physics. For example, in biology, graphs can be used to track the migration paths or movement of animals.)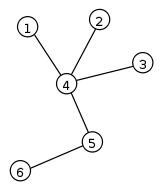
http://en.wikipedia.org/wiki/File:Tree_graph.svg
How does the city of Königsberg relate to graph theory?
The city of Königsberg was a city in Prussia that sat on the Pregel River. There were seven bridges that crossed the river as pictured below. Königsberg relates to graph theory because Leonhard Euler was interested in the question if a route existed where he could walk over each of the seven bridges exactly one time.Euler created a graph of the land (the nodes) and the bridge paths (the vertices) and this bridge problem represented the beginning of graph theory.)
http://www.jcu.edu/math/vignettes/v5im3.gif
Walkthrough
Advanced Placement Lessons
Grade 6 - 12+ Lessons
Grade 3 - 5 Lessons
You need to log in to access this simulation.Grade 6 - 12+ Lessons
