What are the two lab test values that control blood pH?
Our bodies are exquisite biochemical entities that must be kept in homeostasis to function correctly. The thousands of enzymatic reactions which take place within us each second function best, with few exceptions, in a blood pH environment between 7.35 and 7.45. The levels of two substances directly influence blood pH: the bicarbonate ion (HCO3-1) and carbonic acid (H2CO3) that make up the bicarbonate/carbonic acid buffer system.
Blood gas analyzers measure the partial pressure of carbon dioxide (pCO2) and the concentration total (tCO2). Then convert the pCO2 into the carbonic acid concentration by using the solubility coefficient for that gas, multiplying the pCO2 by 0.03, and expressing the carbonic acid concentration as millimoles per liter (mmol/L). Since total CO2 is made up of the bicarbonate ion and carbonic acid, the [HCO3-1] can be calculated by subtracting the [H2CO3] from tCO2 and expressing that value in mmol/L.
How do buffers work?
A buffer is a two-part chemical system that, together, prevents changes in a solution’s pH. Buffers work by converting excess hydrogen ions (H+1) or hydroxide ions (OH-1) added to the solution (which would normally change the pH) into a chemical form that will not change the pH. The two parts of a buffer system are called the conjugate base and the conjugate acid.
- The conjugate base will accept hydrogen, reacting with excess hydrogen ions to become the conjugate acid.
- The conjugate acid can donate a hydrogen, reacting with excess hydroxyl ions to be converted into the conjugate base.
Here is an example of the bicarbonate/carbonic acid buffer system, which is the most important one in our body:
There are more blood buffers besides the bicarbonate/carbonic acid one previously described. Proteins, for example, have amino acids (histidine and arginine) that can accept hydrogen ions to become, themselves, ionized.
This is particularly important in hemoglobin’s buffering action as CO2 enters a red blood cell at the tissue level, combines with water to form H2CO3, and then dissociates into HCO3-1 and H+. This continual influx of excess H+ into the cell could significantly alter the cell’s intracellular pH. Histidines and arginines in hemoglobin take on those H+ ions, thereby buffering the cell’s cytoplasm. Two critical histidines in hemoglobin are strategically placed to hold the heme group, which holds oxygen taken in at the alveoli. When these histidines buffer the hydrogen after CO2 comes into the red blood cell at the tissue level, their 3-D orientation shifts, making them less able to hold their oxygens. Thus, the buffering role of hemoglobin is essential for the release of oxygen to tissues.
It’s all in the ratio!
The Henderson-Hasselbalch (H-H) equation, developed by Lawrence Henderson (U.S., 1908) and Karl Hasselbalch (Denmark, 1916), includes the plasma bicarbonate ion and carbonic acid concentrations in a ratio formula as shown below:
Believe it or not, the ratio of [HCO3-1] to [H2CO3] is the only thing that will determine if a person has one of the four kinds of acid-base imbalances, so knowing the [HCO3-1] and [H2CO3] values is key to determining the primary acid-base problem of a patient.
If you do the H-H calculation in reverse to find out what the ratio of bicarbonate ion concentration to carbonic acid concentration has to be in order to have a normal pH, you will find that the ratio to get pH 7.35 is 17.8 to 1, while the ratio to get pH 7.45 is 22.4 to 1. Try this in the H-H equation for yourself. This can be helpful to remember whenever you have a question that includes only the ratio. You will not know what kind of acidosis or alkalosis the person has, but you can at least know the overall direction (more acidic, more basic) of the patient’s problem. It truly is all about the ratio!
What is the difference between “correction” and “compensation”?
When a person has an acid-base disorder, meaning that their blood pH is becoming either abnormally acidic or alkaline, there are two ways to bring that pH back to within the reference range of 7.35 to 7.45. The best, of course, would be to correct the situation, removing whatever is happening to disrupt the ratio of [HCO3-1] to [H2CO3].
- Note that if the bicarbonate ion numerator decreases as the patient’s primary problem (as in the case of ketoacidosis), the correction would have to make that numerator increase (as in removing the ketoacids from the blood), regardless of what the denominator is.
- Similarly, if the carbonic acid denominator would increase as the patient’s primary problem (as in the case of barbiturate overdose), the correction would have to make the denominator decrease (as in removing the barbiturates).
- But all too often, that correction is not easily accomplished. This is when the process of compensation will attempt to use other means to bring the ratio back to normal. Note that compensation mechanisms can do this without changing the part of the ratio which is the primary problem and always uses the buffer partner not involved in the primary problem.
If compensation creates a second acid-base problem, how can you tell which is the primary problem and which is the compensation?
This is actually a simple question that only requires the information from Table 1.
As an example, consider the following scenario, with reference ranges (RR) in parentheses:
pH = 7.42 (7.35-7.45)
pCO2 = 52 mmHg (35-45 mmHg)
[HCO3-1] = 33 mmol/L (21-28 mmol/L)
- Recall that CO2 is converted into carbonic acid (H2CO3), so CO2 is considered the same as the conjugate acid
- The pH is above 7.40 (the mean of the reference range) so the system is alkaline, therefore either Metabolic Alkalosis (MAlk) or Respiratory Alkalosis (RAlk) is happening as the primary problem.
- An increased pCO2 means Respiratory Acidosis (RAc) is present.
- An increased [HCO2-1] means MAlk is present.
- Both of these acid-base imbalances are happening simultaneously.
- Given these two realities, the primary problem for this patient is MAlk, and the RAc is a compensation.
- Note that you can do this without even knowing the patient’s age, gender, or any other clinical information!
- Since the pH is back within the reference range, this patient has a fully compensated metabolic acidosis. If the compensating buffer partner is moving but the pH is not yet in the reference range, it will be “partially compensated.” If the compensating buffer partner is not moving at all, it will usually be uncompensated.
This thought process will work every time! The only instance where determining the primary problem will be difficult will be when compensation makes the pH become 7.40 since you do not then have the hint of where the original problem placed the patient’s pH before compensation.
How can you calculate the amount of compensation needed to fully compensate an acid-base abnormality?
Here is another instance where it’s all about the ratio! Consider the following scenario:
A male patient, 35 years old, presents with shortness of breath, excessive thirst, disorientation, plasma glucose 373 mg/dL, blood ketones “moderate,” pCO2 = 37 mm Hg (35-45), tCO2 = 15.1 mmol/L
- What is his [H2CO3]? The relationship is [H2CO3] = pCO2 × 0.03, so 37 × 0.03 = 1.11 mmol/L (RR = 1.05 – 1.35 mmol/L, so this value is Normal)
- What is his [HCO3-1]? The relationship is [HCO3-1] = tCO2 – [H2CO3], so 15.1 – 1.11 = 13.99 mmol/L (RR = 21-28 mmol/L) (decreased, so Metabolic Acidosis (MAc) since [H2CO3] should be decreasing but is not)
- What is his ratio of [HCO3-1] to [H2CO3]? 12.6 to 1 (below 17.8 to 1, so predict acidosis)
- What is his blood pH? 6.1 + log (12.6) = 7.20
- Which type is his acid-base imbalance? uncompensated MAc
- Without changing the buffer partner that is at primary fault, what concentration would the compensating buffer partner have to be to make his blood pH be fully compensated?
Buffer partner at fault that cannot be changed = [HCO3-1] (here it is 13.99 mmol/L)
Buffer partner that needs to compensate = [H2CO3]
ratio for 7.35 = 17.8 to 1 so
17.8
1
=
13.99
x
= 0.79 mmol/L [H2CO3] will compensate
NOTE: this ratio is chosen since the primary problem is acidosis
doublecheck: pH = 6.1 + log (13.99/0.79)
= 6.1 + log (17.94)
= 6.1 + 1.25 = 7.35 OK!
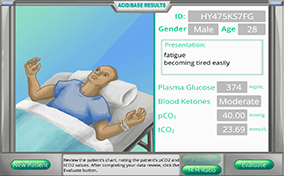 Acid-base balance can be a daunting subject to understand since there are so many biochemical and physiological “players” involved, but determining blood pH and interpreting blood gas test results is actually much simpler than you might think. Your challenges in this module are to correlate changes in blood pH with just two laboratory test results, calculate the values needed to determine blood pH by the Henderson-Hasselbalch formula, identify the primary acid-base problem based on patient test results, determine if compensation (partial or full) is happening or not, predict which buffer partner needs to change in order to compensate, and calculate the amount of buffer partner change needed to fully compensate the acid-base disturbance.
Acid-base balance can be a daunting subject to understand since there are so many biochemical and physiological “players” involved, but determining blood pH and interpreting blood gas test results is actually much simpler than you might think. Your challenges in this module are to correlate changes in blood pH with just two laboratory test results, calculate the values needed to determine blood pH by the Henderson-Hasselbalch formula, identify the primary acid-base problem based on patient test results, determine if compensation (partial or full) is happening or not, predict which buffer partner needs to change in order to compensate, and calculate the amount of buffer partner change needed to fully compensate the acid-base disturbance.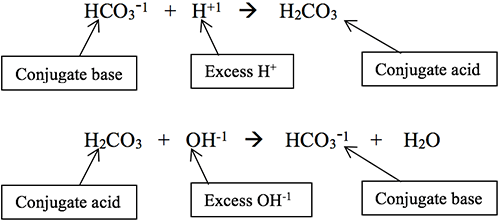) There are more blood buffers besides the bicarbonate/carbonic acid one previously described. Proteins, for example, have amino acids (histidine and arginine) that can accept hydrogen ions to become, themselves, ionized.
There are more blood buffers besides the bicarbonate/carbonic acid one previously described. Proteins, for example, have amino acids (histidine and arginine) that can accept hydrogen ions to become, themselves, ionized.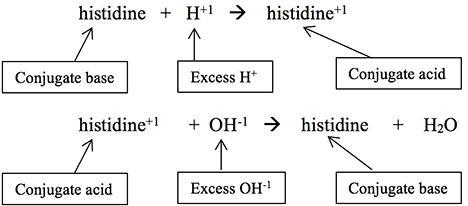) This is particularly important in hemoglobin’s buffering action as CO2 enters a red blood cell at the tissue level, combines with water to form H2CO3, and then dissociates into HCO3-1 and H+. This continual influx of excess H+ into the cell could significantly alter the cell’s intracellular pH. Histidines and arginines in hemoglobin take on those H+ ions, thereby buffering the cell’s cytoplasm. Two critical histidines in hemoglobin are strategically placed to hold the heme group, which holds oxygen taken in at the alveoli. When these histidines buffer the hydrogen after CO2 comes into the red blood cell at the tissue level, their 3-D orientation shifts, making them less able to hold their oxygens. Thus, the buffering role of hemoglobin is essential for the release of oxygen to tissues.
This is particularly important in hemoglobin’s buffering action as CO2 enters a red blood cell at the tissue level, combines with water to form H2CO3, and then dissociates into HCO3-1 and H+. This continual influx of excess H+ into the cell could significantly alter the cell’s intracellular pH. Histidines and arginines in hemoglobin take on those H+ ions, thereby buffering the cell’s cytoplasm. Two critical histidines in hemoglobin are strategically placed to hold the heme group, which holds oxygen taken in at the alveoli. When these histidines buffer the hydrogen after CO2 comes into the red blood cell at the tissue level, their 3-D orientation shifts, making them less able to hold their oxygens. Thus, the buffering role of hemoglobin is essential for the release of oxygen to tissues.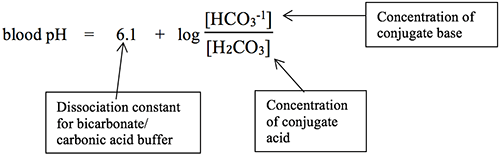) Believe it or not, the ratio of [HCO3-1] to [H2CO3] is the only thing that will determine if a person has one of the four kinds of acid-base imbalances, so knowing the [HCO3-1] and [H2CO3] values is key to determining the primary acid-base problem of a patient.
Believe it or not, the ratio of [HCO3-1] to [H2CO3] is the only thing that will determine if a person has one of the four kinds of acid-base imbalances, so knowing the [HCO3-1] and [H2CO3] values is key to determining the primary acid-base problem of a patient.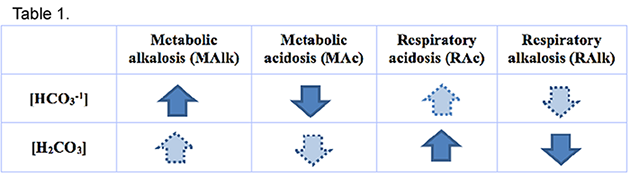) As an example, consider the following scenario, with reference ranges (RR) in parentheses:
As an example, consider the following scenario, with reference ranges (RR) in parentheses: