What is mass?
Mass is defined as the amount of matter in an object. Mass is typically measured in units of grams or kilograms. The mass of an object is constant and does not change based on the location of the object. An object that has a mass of 10-kilograms on Earth would have the same mass on the moon, but the object's weight would be about 1/6 its weight on Earth since the force of gravity on the moon is less than the force of gravity on Earth.
What is volume?
Volume is defined as the amount of space an object takes up. Volume has a wide variety of units of measure, including English measures of gallons, pints, and cubic feet; and metric measures of liter and cubic centimeters.
What is density?
Density can be thought of as the compactness of a material. The more compact the material, the higher the material's density. Density is defined as the mass of an object divided by its volume. Common units of density are grams per milliliter or grams per cubic centimeter.
Why do some objects sink and other objects float?
The sinking or floating of an object placed in a fluid depends entirely on the comparison of the density of the object versus the density of the fluid. A denser object will sink in a less dense fluid. A less dense object will float on a more dense fluid. If the object's and fluid's densities are identical, the object will hover in position at whatever depth the object is released in the fluid.
What information does the slope of a line provide?
The slope of a line provides information about how two variables are related. The slope is defined as the rise of the line (change in the "y" variable) over the run of the line (change in the "x" variable). A steep slope indicates that the "y" variable changes drastically, while the "x" variable changes much less. A near flat slope shows that the "y" variable changes little, while the "x" variable changes greatly.
How can a line graph be used to predict unknown values?
Graphs provide a way to quickly analyze the relationship between variables. Graphs are typically constructed using two axes, the "y" axis where the dependent variable is plotted and the "x" axis where the independent is plotted. A line graph is constructed by plotting each "x" and "y" value, then connecting each point with a line. Best fit lines are constructed by drawing the "average" line through the points without connecting each point. Values of x and y that were not collected in the data set can be estimated by choosing any point on the line and drawing a horizontal line to the "y" axis to determine the y value and dropping a vertical line from the point to the "x" axis to predict the x value.
Here are some definitions to help you in your Grade 3-5 Lesson 1 investigation.
Matter - anything that has mass and takes up space
Mass - the amount of matter in something
Volume - the amount of space something takes up
Density - the compactness of something
Observation - the use of one of the senses to collect information about something
Senses - sight, hearing, smell, touch, and taste
Inference - a conclusion based on evidence
Estimate - to form an opinion about something’s size
Here are some definitions to help you in your Grade 3-5 Lesson 2 investigation.
Density - the compactness of something
Hexagonal - a shape with six sides
Triangular - a shape with three sides
Square - a shape with four side
Trials - the number of times a given experiment is repeated
Data - information collected for studying
Claim - a statement based on observations and evidence
Evidence - information, facts, or data supporting a claim
Conclusion - a final claim based on reviewing the data and evidence
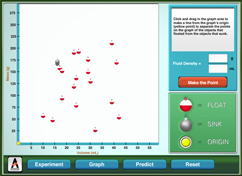Fluids have a number of characteristics that can be used for identification, such as boiling point, freezing point, and viscosity. One of the most common properties used to identify a fluid is density. Can simply dropping various items in a fluid and some basic understanding of graphing be used to determine the fluid’s density? Don’t drop the ball, try out the simulation.
